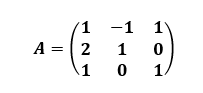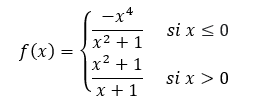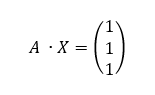Este es el examen oficial de Matemáticas CCSS 2023 de la convocatoria ordinaria en la Comunidad de Madrid con los enunciados y soluciones en la parte inferior de esta página. Podrás comprobar tu nivel y conocer el contenido y nivel de las pruebas. Si deseas prepararte con nosotros con nuestro curso EBAU / EVAU, pregúntanos y te informaremos.
EXAMEN DE MATEMÁTICAS CCSS 2023
EXAMEN OFICIAL SELECTIVIDAD EBAU REALIZADO EN MADRID EN LA CONVOCATORIA 2022/2023
A.1. (2 puntos) Se considera la matriz
- a) Estudie si la matriz A es invertible y, en caso afirmativo, calcule su inversa.
- b) Determine la matriz X tal que
A.2. (2 puntos) Se considera la función real de variable real definida por la siguiente expresión:
(x)= 6x²+ae×-2,a∈ R
- a) Obtenga el valor del parámetro real a sabiendo que ∫¹ f(x)dx= e-1
- b) Para a = 1, obtenga la ecuación de la recta tangente a la gráfica de f(x) en el punto de abscisa x=0
A.3. (2 puntos) Se considera la función real de variable real definida por la siguiente expresión:
- a) Indique el dominio de la función f(x) y analice su continuidad, señalando el tipo de discontinuidad si la presenta.
- b) Determine las asíntotas de la función anterior
A.4. (2 puntos) Sean dos sucesos A y B tales que P(A) = 0, 55 y P(B) = 0, 1. Además se sabe que P (| A) = 0, 89, donde es el suceso complementario de B. Calcule las siguientes probabilidades:
- a) P (A ∩ B).
- b) P (∩ ), siendo el suceso complementario de A .
A.5. (2 puntos) La capacidad en mililitros de un bote de champú se puede aproximar por una variable aleatoria con distribución normal de media µ y desviación típica igual a 10 ml.
- a) Se toma una muestra aleatoria de tamaño 20 y se obtiene que su media muestral es de 200 ml. Determine un intervalo de confianza del 95 % para la capacidad media de los botes de champú.
- b) Determine el tamaño mínimo de la muestra para que el error máximo cometido en la estimación de la media sea menor que 0,5 mililitros, con un nivel de confianza del 90 %.
B.1. (2 puntos) Una pastelería tiene 220 buñuelos de chocolate, nata y crema. Hay el doble de buñuelos de nata que de crema. Además, el doble de la cantidad de los buñuelos de crema más el triple de los buñuelos de chocolate es igual al doble de la cantidad de los buñuelos de nata. Calcule la cantidad de buñuelos que hay de cada tipo.
B.2. (2 puntos) Se desea producir pintura verde en dos tonalidades, VERDE1 y VERDE2, mezclando pintura azul y amarilla en distintas proporciones. Un litro de pintura VERDE1 necesita 0,3 litros de azul y 0,7 litros de amarillo, mientras que un litro de pintura VERDE2 necesita 0,5 litros de azul y 0,5 litros de amarillo. Actualmente se dispone de 20 litros de azul y 28 litros de amarillo. El beneficio por litro de la pintura VERDE1 es de 1 euro, y por litro de pintura VERDE2 es de 1,2 euros. No se pueden producir más de 30 litros de pintura VERDE1. ¿Cuántos litros de pintura VERDE1 y VERDE2 debe producir para maximizar sus beneficios? ¿Cuál será el beneficio obtenido?
B.3. (2 puntos) Se consideran las siguientes funciones reales de variable real:
f(x)= -x³+ 2x ² +4x, g(x)=4x
- a) Determine los intervalos de crecimiento y decrecimiento de la función f(x).
- b) Calcule el área de la región acotada limitada por las gráficas de las funciones f(x) y g(x) en el primer cuadrante del plano cartesiano.
B.4. (2 puntos) El Ministerio de Educación y Formación Profesional convoca regularmente unas ayudas al estudio. En el curso 2019-2020 las ayudas destinadas a las Enseñanzas Obligatorias representaron el 56,5 % del total, el 24 % correspondieron a Enseñanzas Universitarias, mientras que el 19, 5 % restante fueron para Enseñanzas Postobligatorias No Universitarias. Las ayudas concedidas son financiadas o bien por el ministerio o bien por la Comunidad Autónoma a la que pertenece el estudiante. Concretamente, en el curso 2019-2020, las ayudas financiadas por el ministerio representaron el 13,8 % del total de ayudas de Enseñanzas Obligatorias, el 86,1% de las Universitarias y el 80,3 % de las Postobligatorias No Universitarias. Eligiendo una ayuda al estudio al azar de las anteriormente descritas, calcule la probabilidad de que:
- a) Sea financiada por el ministerio.
- b) La ayuda sea de Enseñanza Obligatoria, sabiendo que ha sido financiada por el ministerio.
B.5. (2 puntos) El 30 % de los individuos de una población tienen una titulación universitaria. Se escoge una muestra al azar de 120 individuos.
- a) ¿Cuál es la distribución aproximada que sigue la proporción de individuos con titulación universitaria de la muestra?
- b) Halle la probabilidad de que más del 35 % de los individuos de la muestra sean titulados universitarios.